四升五年级数奥数讲义_鸡兔同笼初步(讲师版)
学科培优数学鸡兔同笼初步学生姓名授课日期教师姓名授课时长知识定位你以前听说过“鸡兔同笼”问题吗?这个问题,是我国古代著名趣题之一。大约在1500年前,《孙子算经》中就记载了这个有趣的问题。书中是这样叙述的:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有35个头;从下面数,有94只脚。求笼中各有几只鸡和兔?重点难点:1.假设法的运用2.鸡兔同笼的变形与解答3.鸡兔同笼的区分考点:1.三者以上的鸡兔同笼问题2.假设法的应用知识梳理解答思路是这样的:假如砍去每只鸡、每只兔一半的脚,则每只鸡就变成了“独角鸡”,每只兔就变成了“双脚兔...
相关推荐
-
小升初名校奥数真题及答案VIP免费

 2024-11-09 39
2024-11-09 39 -
2023-2024学年七年级下册数学第一章第七节试卷及答案北师大版VIP免费

 2024-11-09 70
2024-11-09 70 -
七年级下册地理第四章试卷及答案人教版VIP免费

 2024-11-10 50
2024-11-10 50 -
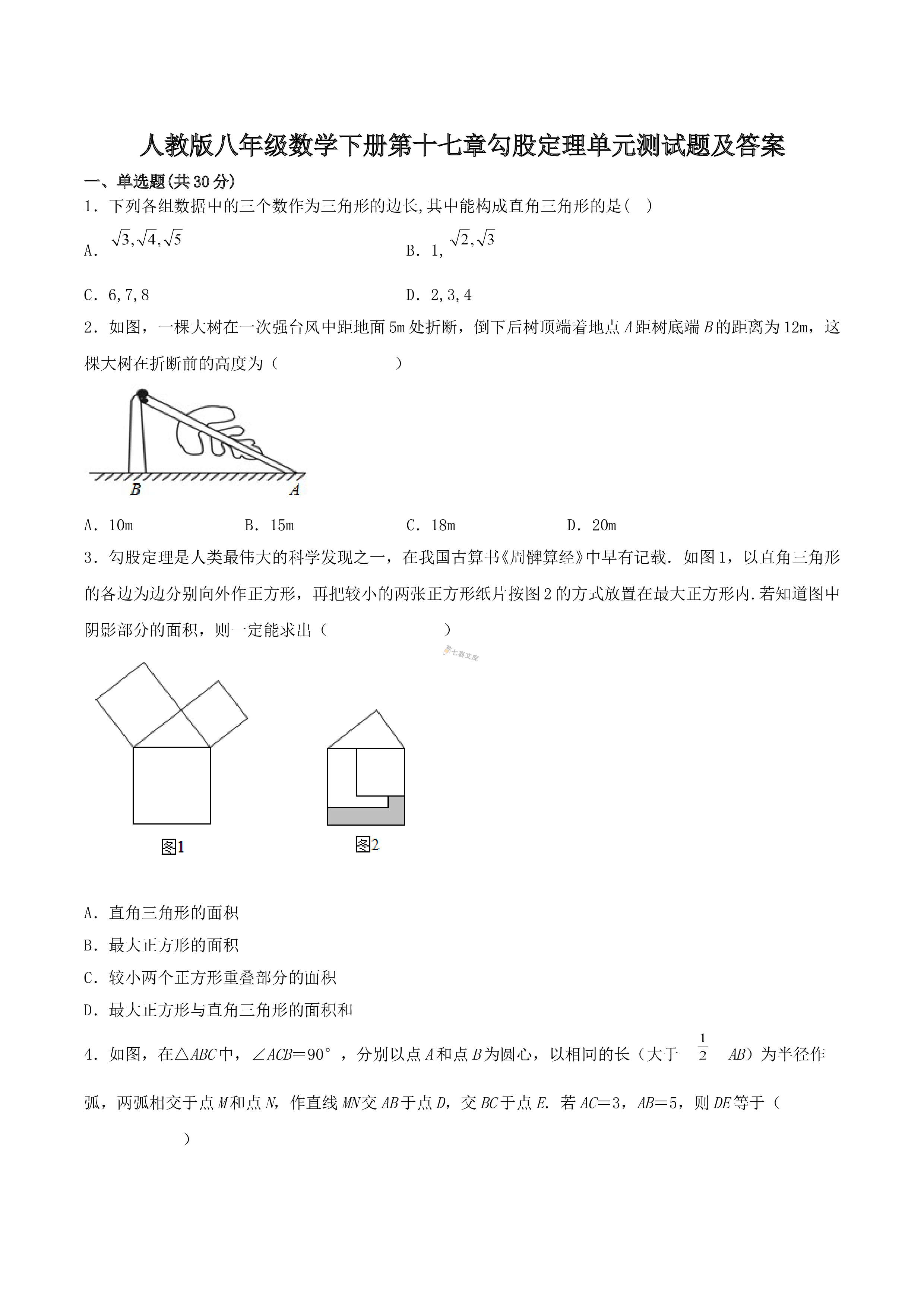
人教版八年级数学下册第十七章勾股定理单元测试题及答案VIP免费
 2024-11-10 427
2024-11-10 427 -
2011年成人高考专升本生态学基础考试真题及答案VIP免费

 2024-11-12 43
2024-11-12 43 -
2023年武汉工程大学教育管理学考研真题VIP免费

 2024-11-14 17
2024-11-14 17 -
2009年江西宜春中考历史真题及答案

 2024-12-24 7
2024-12-24 7 -
2020年贵州铜仁中考历史真题及答案

 2025-01-04 5
2025-01-04 5 -
2020年贵州铜仁中考生物真题及答案

 2025-01-04 4
2025-01-04 4 -
2020年贵州铜仁中考数学真题及答案

 2025-01-04 6
2025-01-04 6
相关内容
-

2020年贵州铜仁中考地理真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考化学真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考历史真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考生物真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考数学真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币






