初一数学暑假讲义 第7讲.一元一次方程的解法及应用.学生版
定义示例剖析等式的概念:用等号来表示相等关系的式子,叫做等式.等式的类型恒等式:无论用什么数值代替等式中的字母,等式总能成立.条件等式:只能用某些数值代替等式中的字母,等式才能成立.矛盾等式:无论用什么数值代替等式中的字母,等式都不能成立.方程需要才成立.如,,.等式性质1:等式两边都加上(或减去)同一个数(或式子),所得结果仍是等式.等式性质2:等式两边都乘以(或除以)同一个数(除数不能是0),结果仍是等式.若,则.若,则,若且,则.在等式变形中,以下两个性质也经常用到:①等式具有对称性,即:如果,那么;②等式具有传递性,即:如果,,那么.【例1】下列各式中,哪些是等式?是等式的请指出类型....
相关推荐
-
小升初名校奥数真题及答案VIP免费

 2024-11-09 43
2024-11-09 43 -
2023-2024学年七年级下册数学第一章第七节试卷及答案北师大版VIP免费

 2024-11-09 96
2024-11-09 96 -
七年级下册地理第四章试卷及答案人教版VIP免费

 2024-11-10 53
2024-11-10 53 -
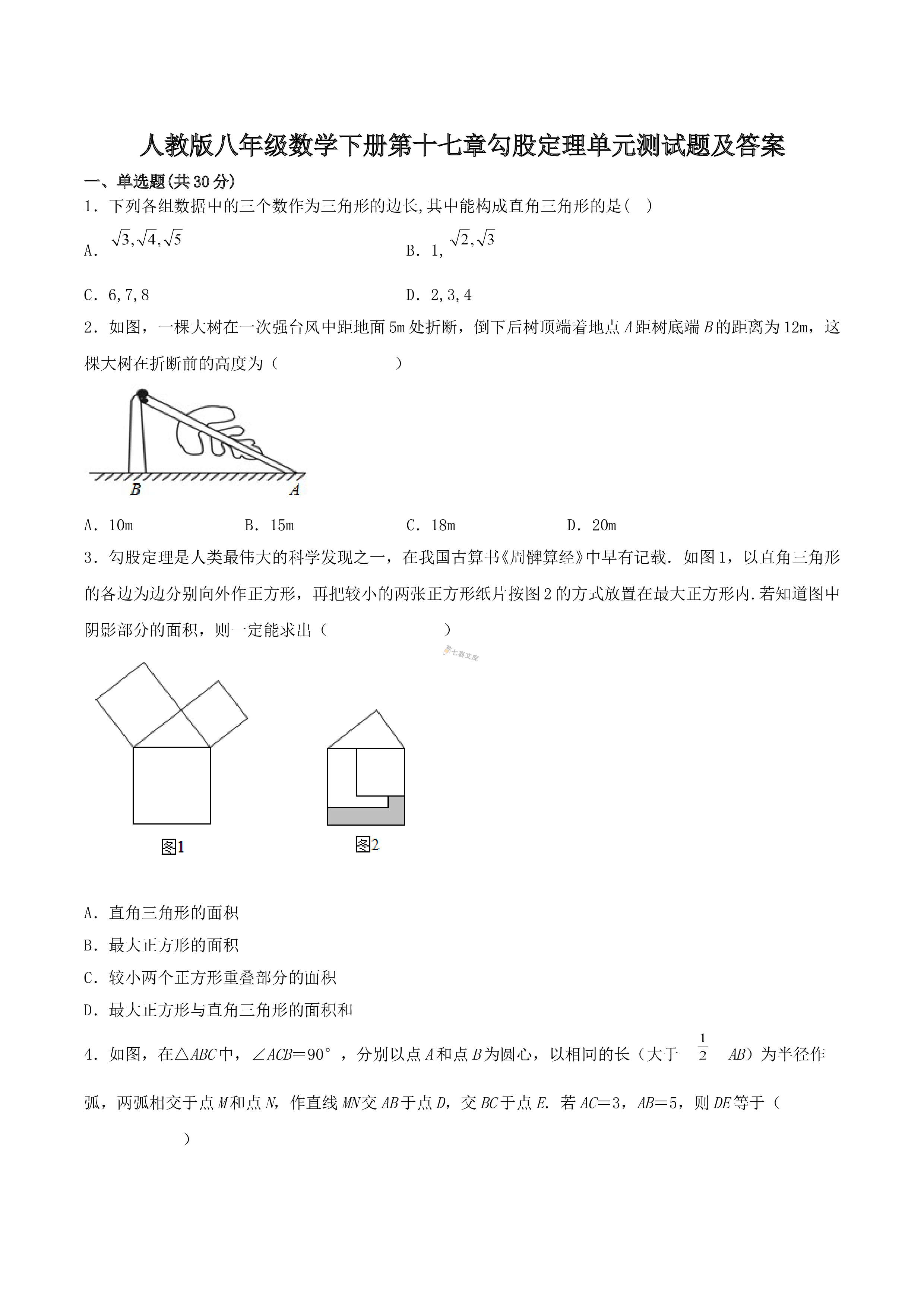
人教版八年级数学下册第十七章勾股定理单元测试题及答案VIP免费
 2024-11-10 437
2024-11-10 437 -
2011年成人高考专升本生态学基础考试真题及答案VIP免费

 2024-11-12 47
2024-11-12 47 -
2023年武汉工程大学教育管理学考研真题VIP免费

 2024-11-14 18
2024-11-14 18 -
2024上半年教师资格证中学综合素质真题及答案VIP免费

 2024-11-17 202
2024-11-17 202 -
2009年江西宜春中考历史真题及答案

 2024-12-24 13
2024-12-24 13 -
2020年贵州铜仁中考生物真题及答案

 2025-01-04 16
2025-01-04 16 -
2020年贵州铜仁中考数学真题及答案

 2025-01-04 17
2025-01-04 17
相关内容
-

2020年贵州铜仁中考地理真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考化学真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考历史真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考生物真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考数学真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币






