2001考研数学三真题及答案
VIP免费
3.0
2024-11-14
0
0
1.53MB
21 页
3.3金币
侵权投诉
2001考研数三真题及答案
一、填空题
(1) 设生产函数为 , 其中
Q
是产出量,
L
是劳动投入量,
K
是资本投入量,而
A
,
α
,
β
均为大于零的参数,则当
Q
=1时
K
关于
L
的弹性为
(2) 某公司每年的工资总额比上一年增加20%的基础上再追加2 百万.若以 表示第
t
年
的
工资总额(单位:百万元),则 满足的差分方程是___
(3) 设矩阵 且秩(
A
)=3,则
k
=
(4) 设随机变量
X
,
Y
的数学期望都是2,方差分别为1和4,而相关系数为0.5.则根据切比雪夫
不
等式 .
(5) 设总体X服从正态分布 而 是来自总体X的简单随机样本,则
随
机变量 服从___分布,参数为_______
二、选择题
(1) 设函数
f
(
x
)的导数在
x
=
a
处连续,又 则( )
(A)
x
=
a
是
f
(
x
)的极小值点.
(B)
x
=
a
是
f
(
x
)的极大值点.
(C) (
a
,
f
(
a
))是曲线
y
=
f
(
x
)的拐点.
(D)
x
=
a
不是
f
(
x
)的极值点, (
a
,
f
(
a
))也不是曲线
y
=
f
(
x
)的拐点.
(2) 设函数 其中 则
g
(
x
)在区间(0,2) 内(
)
(A)无界 (B)递减 (C) 不连续 (D) 连续
(3) 设
其中
A
可逆,则 等于( )
(A)
(B) (C) (D) .
(4) 设
A
是
n
阶矩阵,α是
n
维列向量.若秩 秩 ,则线性方程组( )
AX
=α必有无穷多解
AX
=α 必有惟一解.
仅有零解 必有非零解.
(5) 将一枚硬币重复掷
n
次,以
X
和
Y
分别表示正面向上和反面向上的次数,则
X
和
Y
的相关系
数等于( )
(A) -1 (B) 0 (C) (D) 1
三 、(本题满分5 分)
设
u
=
f
(
x
,
y
,
z
)有连续的一阶偏导数,又函数
y
=
y
(
x
)及
z
=
z
(
x
)分别由下列两式确定:
和 求
四 、(本题满分6 分)
已知
f
(
x
)在( ∞,+∞)−内可导,且 求
c
的值.
五 、(本题满分6 分)
求二重积分 的值,其中
D
是由直线
y
=
x
,
y
= 1−及
x
=1围成的平面
区域
六、(本题满分7 分)
已知抛物线 (其中
p
<0,
q
>0)在第一象限与直线
x
+
y
=5相切,且此抛物线与
x
轴所围成的平面图形的面积为S.
(1) 问
p
和
q
为何值时,S达到最大? (2)求出此最大值.
七、(本题满分6 分)
设
f
(
x
)在区间[0,1]上连续,在(0,1)内可导,且满足
证明:存在ξ∈(0,1), 使得
八、(本题满分7 分)
已知 满足 (
n
为正整数)且 求函数项级数
之和.
九、(本题满分9 分)
设矩阵 已知线性方程组
AX
=β有解但不唯一,试求:
(1)
a
的值;
(2) 正交矩阵Q,使 为对角矩阵.
十、(本题满分8 分)
设
A
为
n
阶实对称矩阵,秩(A)=n, 是 中元素的代数余子式(
i
,
j
=1,2,…,
n
),二次型
(1) 记 把 写成矩阵形式,并证明二
次型的矩阵为 ;
(2) 二次型与 的规范形是否相同?说明理由.
十一、(本题满分8 分)
生产线生产的产品成箱包装,每箱的重量是随机的,假设每箱平均重50 千克,标准差为5
千克.若用最大载重量为5 吨的汽车承运,试利用中心极限定理说明每辆车最多可以装多少
箱,才能保障不超载的概率大于0.977. (Φ(2)=0.977,其中Φ(
x
) 是标准正态分布函数).
十二、(本题满分8 分)
设随机变量X 和Y 对联和分布是正方形
G
={(
x
,
y
)|1≤
x
≤3,1≤
y
≤3}上的均匀分布,试
相关推荐
-
小升初名校奥数真题及答案VIP免费

 2024-11-09 41
2024-11-09 41 -
2023-2024学年七年级下册数学第一章第七节试卷及答案北师大版VIP免费

 2024-11-09 84
2024-11-09 84 -
七年级下册地理第四章试卷及答案人教版VIP免费

 2024-11-10 51
2024-11-10 51 -
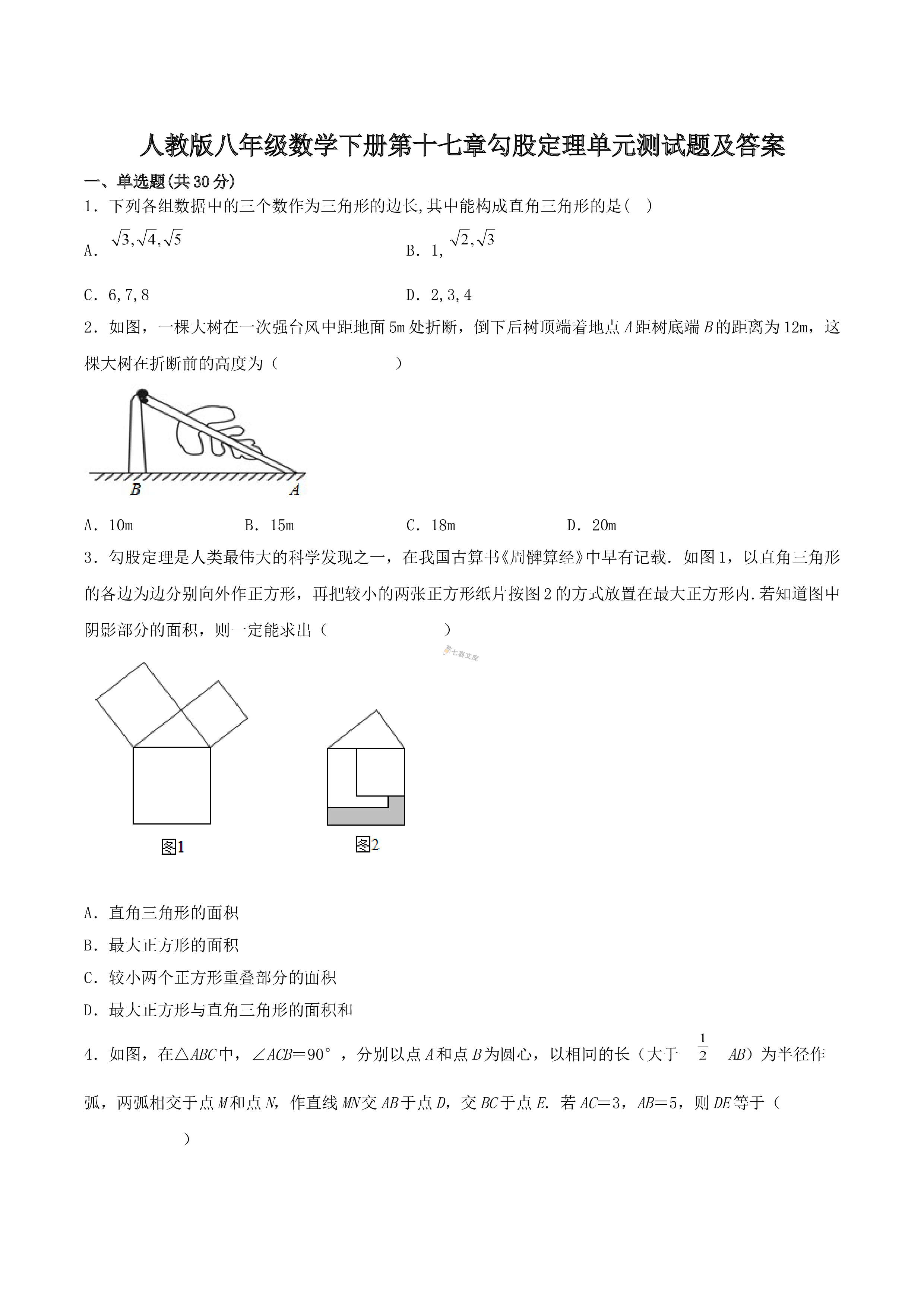
人教版八年级数学下册第十七章勾股定理单元测试题及答案VIP免费
 2024-11-10 427
2024-11-10 427 -
2011年成人高考专升本生态学基础考试真题及答案VIP免费

 2024-11-12 43
2024-11-12 43 -
2023年武汉工程大学教育管理学考研真题VIP免费

 2024-11-14 17
2024-11-14 17 -
2009年江西宜春中考历史真题及答案

 2024-12-24 8
2024-12-24 8 -
2020年贵州铜仁中考历史真题及答案

 2025-01-04 5
2025-01-04 5 -
2020年贵州铜仁中考生物真题及答案

 2025-01-04 6
2025-01-04 6 -
2020年贵州铜仁中考数学真题及答案

 2025-01-04 8
2025-01-04 8
分类:行业题库
价格:3.3金币
属性:21 页
大小:1.53MB
格式:DOC
时间:2024-11-14
相关内容
-

2020年贵州铜仁中考地理真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考化学真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考历史真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考生物真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考数学真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币






