2002考研数学三真题及答案
VIP免费
3.0
2024-11-14
0
0
1.59MB
19 页
3.3金币
侵权投诉
2002 考研数学三真题及答案
一、填空题(本题共 5 小题,每小题 3 分,满分 15 分,把答案填在题中横线上)
(1) 设常数 ,则
(2) 交换积分次序: .
(3) 设三阶矩阵 ,三维列向量 .已知 与 线性相关,
则
.
(4) 设随机变量 和 的联合概率分布为
-1 0 1
0 0.07 0.18 0.15
1 0.08 0.32 0.20
则 和 的协方差 .
(5) 设总体 的概率密度为
而 是来自总体 的简单随机样本,则未知参数 的矩估计量为
二、选择题(本题共 5 小题,每小题 3 分,共 15 分,在每小题给出的四个选项中,只有一项
符合题目要求,把所选项前的字母填在题后的括号内.)
(1) 设函数 在闭区间 上有定义,在开区间 内可导,则 ( )
(A)当 时,存在 ,使 .
(B)对任何 ,有 .
(C)当 时,存在 ,使 .
(D)存在 ,使 .
(2) 设幂级数 与 的收敛半径分别为 与 ,则幂级数 的收敛
半径为 ( )
(A) 5 (B) (C) (D)
(3) 设 是 矩阵, 是 矩阵,则线性方程组 ( )
(A)当 时仅有零解 (B)当 时必有非零解
(C)当 时仅有零解 (D)当 时必有非零解
(4) 设 是 阶实对称矩阵, 是 阶可逆矩阵,已知 维列向量 是 的属于特征值
的
特征向量,则矩阵 属于特征值 的特征向量是 ( )
(A) (B) (C) (D)
(5) 设随机变量 和 都服从标准正态分布,则 ( )
(A) 服从正态分布 (B) 服从 分布
(C) 和 都服从 分布 (D) 服从 分布
三、(本题满分 5 分)
求极限
四、(本题满分 7 分)
设函数 有连续偏导数,且 由方程 所确定,求
.
五、(本题满分 6 分)
设 求 .
六、(本题满分 7 分)
设 是由抛物线 和直线 及 所围成的平面区域; 是由抛
物线 和直线 所围成的平面区域,其中 .
(1)试求 绕 轴旋转而成的旋转体体积 ; 绕 轴旋转而成的旋转体体积 ;
(2)问当 为何值时, 取得最大值?试求此最大值.
七、(本题满分 7 分)
(1)验证函数 满足微分方程
(2)利用(1)的结果求幂级数 的和函数.
八、(本题满分 6 分)
设函数 在 上连续,且 .利用闭区间上连续函数性质,证明存
在一点 ,使 .
九、(本题满分 8 分)
设齐次线性方程组
其中 ,试讨论 为何值时,方程组仅有零解、有无穷多组解?在有无
穷多组解时,求出全部解,并用基础解系表示全部解.
十、(本题满分 8 分)
设 为三阶实对称矩阵,且满足条件 ,已知 的秩
(1)求 的全部特征值
(2)当 为何值时,矩阵 为正定矩阵,其中 为三阶单位矩阵.
十一、(本题满分 8 分)
假设随机变量 在区间 上服从均匀分布,随机变量
试求:(1) 和 的联合概率分布;(2) .
十二、(本题满分 8 分)
假设一设备开机后无故障工作的时间 服从指数分布,平均无故障工作的时间
相关推荐
-
小升初名校奥数真题及答案VIP免费

 2024-11-09 41
2024-11-09 41 -
2023-2024学年七年级下册数学第一章第七节试卷及答案北师大版VIP免费

 2024-11-09 84
2024-11-09 84 -
七年级下册地理第四章试卷及答案人教版VIP免费

 2024-11-10 51
2024-11-10 51 -
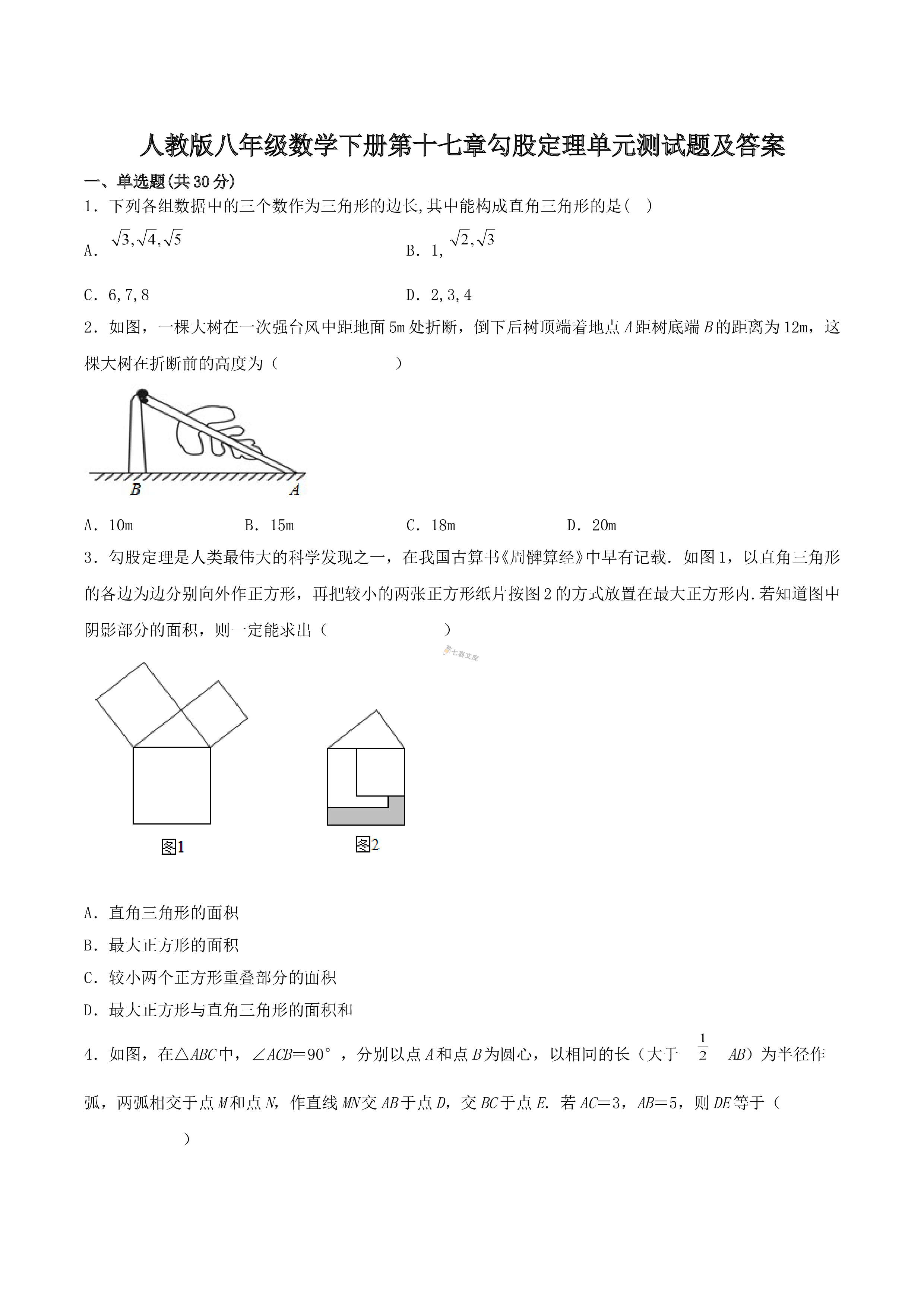
人教版八年级数学下册第十七章勾股定理单元测试题及答案VIP免费
 2024-11-10 427
2024-11-10 427 -
2011年成人高考专升本生态学基础考试真题及答案VIP免费

 2024-11-12 43
2024-11-12 43 -
2023年武汉工程大学教育管理学考研真题VIP免费

 2024-11-14 17
2024-11-14 17 -
2009年江西宜春中考历史真题及答案

 2024-12-24 8
2024-12-24 8 -
2020年贵州铜仁中考历史真题及答案

 2025-01-04 5
2025-01-04 5 -
2020年贵州铜仁中考生物真题及答案

 2025-01-04 6
2025-01-04 6 -
2020年贵州铜仁中考数学真题及答案

 2025-01-04 8
2025-01-04 8
分类:行业题库
价格:3.3金币
属性:19 页
大小:1.59MB
格式:DOC
时间:2024-11-14
相关内容
-

2020年贵州铜仁中考地理真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考化学真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考历史真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考生物真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考数学真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币






