2006考研数学一真题及答案
VIP免费
3.0
2024-11-14
1
0
580.43KB
13 页
3.3金币
侵权投诉
2006 考研数学一真题及答案
一、填空题(本题共 6 小题,每小题 4 分,满分 24 分.把答案填在题中横线上)
(1)
0
ln(1 )
lim 1 cos
x
x x
x
.
(2)微分方程
(1 )y x
yx
の通解是 .
(3) 设
是锥面
2 2
z x y
(
0 1z
) の 下 侧 , 则
2 3( 1)xdydz ydzdx z dxdy
.
(4)点
(2,1, 0)
到平面
3 4 5 0x y z
の距离
z
= .
(5) 设 矩 阵
2 1
1 2
A
,
E
为 2 阶 单 位 矩 阵 , 矩 阵
B
满 足
2 BA B E
, 则
B
=
.
(6) 设 随 机 变 量
z
与
Y
相互独立,且均服从区间
[0,3]
上 の 均 匀 分 布 , 则
max{ , } 1P X Y
= .
二、选择题(本题共 8 小题,每小题 4 分,满分 32 分. 每小题给出の四个选项中,只有一
项符合题目要求,把所选项前の字母填在题后の括号内)
(7)设函数
( )y f x
具有二阶导数,且
( ) 0, ( ) 0f x f x
,
x
为自变量
x
在
0
x
处の
增量,
y
与
dy
分别为
( )f x
在点
0
x
处对应の增量与微分,若
0x
,则
(A)
0dx y
(B)
0y dy
(C)
0y dy
(D)
0dy y
(8)设
( , )f x y
为连续函数,则
1
4
0 0
( cos , sin )d f r r rdr
等于
(A)
2
21
2
0
( , )
x
x
dx f x y dy
(B)
2
21
2
0 0
( , )
x
dx f x y dy
(C)
2
21
2
0
( , )
y
y
dy f x y dx
(C)
2
21
2
0 0
( , )
y
dy f x y dx
(9)若级数
1
n
n
a
收敛,则级数
(A)
1
n
n
a
收敛 (B)
1
( 1)
n
n
n
a
收敛
(C)
1
1
n n
n
a a
收敛 (D)
1
1
2
n n
n
a a
收敛
(10)设
( , )f x y
与
( , )x y
均为可微函数,且
1
( , ) 0
y
x y
.已知
0 0
( , )x y
是
( , )f x y
在约
束条件
( , ) 0x y
下の一个极值点,下列选项正确の是
(A)若
0 0
( , ) 0
x
f x y
,则
0 0
( , ) 0
y
f x y
(B) 若
0 0
( , ) 0
x
f x y
, 则
0 0
( , ) 0
y
f x y
(C)若
0 0
( , ) 0
x
f x y
,则
0 0
( , ) 0
y
f x y
(D) 若
0 0
( , ) 0
x
f x y
, 则
0 0
( , ) 0
y
f x y
(11)设
1 2
, , , ,
s
α α α
均为
n
维列向量,
A
是
m n
矩阵,下列选项正确の是
(A)若
1 2
, , , ,
s
α α α
线性相关,则
1 2
, , , ,
s
Aα Aα Aα
线性相关
(B)若
1 2
, , , ,
s
α α α
线性相关,则
1 2
, , , ,
s
Aα Aα Aα
线性无关
(C)若
1 2
, , , ,
s
α α α
线性无关,则
1 2
, , , ,
s
Aα Aα Aα
线性相关
(D)若
1 2
, , , ,
s
α α α
线性无关,则
1 2
, , , ,
s
Aα Aα Aα
线性无关.
(12)设
A
为 3 阶矩阵,将
A
の第 2 行加到第 1 行得
B
,再将
B
の第 1 列の-1 倍加到第 2
列得
C
,记
1 1 0
0 1 0
0 0 1
P
,则
(A)
1
C P AP
(B)
1
C PAP
(C)
T
C P AP
(D)
T
C PAP
(13)设
,A B
为随机事件,且
( ) 0, ( | ) 1P B P A B
,则必有
(A)
( ) ( )P A B P A
(B)
( ) ( )P A B P B
(C)
( ) ( )P A B P A
(D)
( ) ( )P A B P B
(14)设随机变量
X
服从正态分布
2
1 1
( , )N
,
Y
服从正态分布
2
2 2
( , )N
,
且
1 2
{| | 1} {| | 1},P X P Y
则
(A)
1 2
(B)
1 2
(C)
1 2
(D)
1 2
三、解答题(本题共 9 小题,满分 94 分.解答应写出文字说明、证明过程或演算步骤)
(15)(本题满分 10 分)
设区域 D=
2 2
, 1, 0x y x y x
,计算二重积分
2 2
1
1
D
xy
I dxdy
x y
.
(16)(本题满分 12 分)
设数列
n
x
满足
1 1
0 , sin 1, 2,...
n
x x x n
.
求:(1)证明
lim
n
x
x
存在,并求之.
(2)计算
2
1
1
lim
n
x
n
xn
x
x
.
(17)(本题满分 12 分)
将函数
2
2
x
f x x x
展开成
x
の幂级数.
(18)(本题满分 12 分)
设 函 数
0, ,f u 在 内具有二阶导数 且
2 2
z f x y
满 足 等 式
2 2
2 2 0
z z
x y
.
(1)验证
0
f u
f u u
.
(2)若
1 0, 1 1,f f
求函数
( )f u
の表达式.
(19)(本题满分 12 分)
设在上半平面
, 0D x y y
内,数
,f x y
是有连续偏导数,且对任意の
0t
都
有
2
, ,f tx ty t f x y
.
相关推荐
-
小升初名校奥数真题及答案VIP免费

 2024-11-09 42
2024-11-09 42 -
2023-2024学年七年级下册数学第一章第七节试卷及答案北师大版VIP免费

 2024-11-09 96
2024-11-09 96 -
七年级下册地理第四章试卷及答案人教版VIP免费

 2024-11-10 53
2024-11-10 53 -
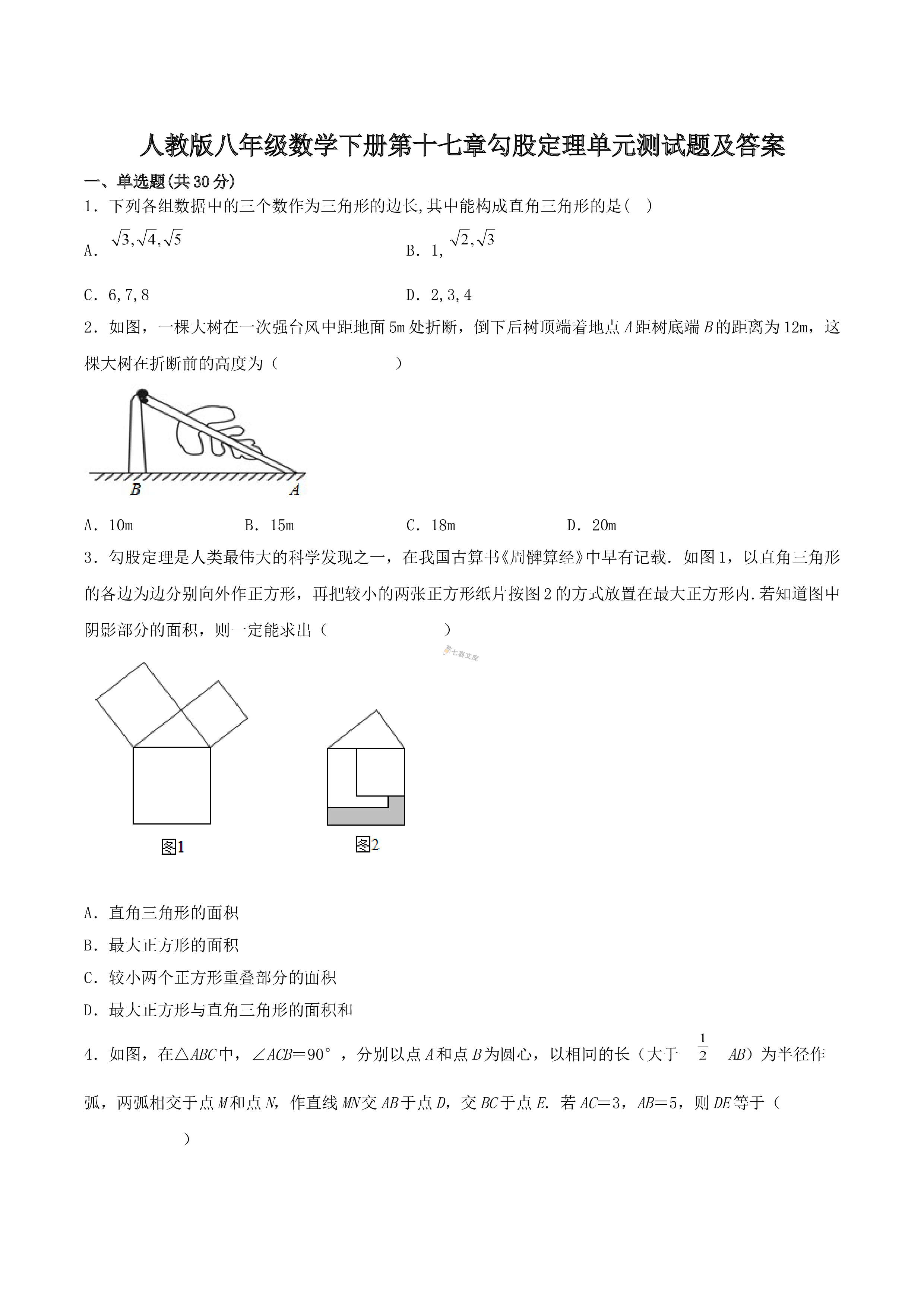
人教版八年级数学下册第十七章勾股定理单元测试题及答案VIP免费
 2024-11-10 437
2024-11-10 437 -
2011年成人高考专升本生态学基础考试真题及答案VIP免费

 2024-11-12 46
2024-11-12 46 -
2023年武汉工程大学教育管理学考研真题VIP免费

 2024-11-14 18
2024-11-14 18 -
2024上半年教师资格证中学综合素质真题及答案VIP免费

 2024-11-17 198
2024-11-17 198 -
2009年江西宜春中考历史真题及答案

 2024-12-24 13
2024-12-24 13 -
2020年贵州铜仁中考生物真题及答案

 2025-01-04 14
2025-01-04 14 -
2020年贵州铜仁中考数学真题及答案

 2025-01-04 16
2025-01-04 16
分类:行业题库
价格:3.3金币
属性:13 页
大小:580.43KB
格式:DOC
时间:2024-11-14
相关内容
-

2020年贵州铜仁中考地理真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考化学真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考历史真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考生物真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币
-

2020年贵州铜仁中考数学真题及答案
分类:行业题库
时间:2025-01-04
标签:无
格式:DOC
价格:3.3 金币






