2011考研经济类联考真题及答案
VIP免费
3.0
2024-11-14
0
0
257.05KB
7 页
3.3金币
侵权投诉
2011 考研经济类联考真题及答案
二、数学单项选择题（本大题共 10 小题，每小题 2.5 分，共 25 分）
21、设
f(x)=arccos(x2)
，则
f'(x)=
（ ）
（A）
−1
√
1−x2
（B）
−2x
√
1−x2
（C）
−1
√
1−x4
（D）
−2x
√
1−x4
【答案】D
【解析】
函数可以看做一个复合函数：
{
y=arccos t¿ ¿¿¿
，根据复合函数求导法则有：
f'(x)= yt
'⋅tx
'=− 1
√
1−t2⋅2x=− 2x
√
1−x4
。
因此选择 D。
22、不定积分
∫x
√
1−x2dx=
（ ）
（ A ）
√
1−x2+C
（ B ）
−1
3
√
(1−x2)3+C
（C）
x
√
1−x2+C
（ D ）
−1
3x
√
(1−x2)3+C
【答案】B
【解析】
方法一：
由于被积函数中含有
√
1−x2
这个结构，可以利用三角换元，可以有：
∫x
√
1−x2dx =
x=sin θ∫sin θcosθd (sin θ)=∫sinθcos2θdθ=−∫cos2θd (cos θ)=−1
3cos3θ+C
=
cos θ=
√
1−x2
−1
3
√
(1−x2)3+C
方法二：
∫x
√
1−x2dx=1
2∫
√
1−x2d(x2)=− 1
2∫
√
1−x2d(1−x2)
，令
t=1−x2
，则有：
−1
2∫
√
t dt=− 1
2×2
3t
3
2+C=− 1
3t
3
2+C
。
因此原式为：
−1
3t
3
2+C=− 1
3
√
(1−x2)3+C
【快捷解法】
由于本题是不定积分，可以有选项求导来进行排除。
对于 A 项，求导得：
(
√
1−x2+C)'=1
2
1
√
1−x2⋅(−2x)
，很明显不正确。
对于 B 项，求导得：
(− 1
3
√
(1−x2)3+C)'=− 1
3×3
2
√
1−x2×(−2x)=x
√
1−x2
，因此选择 B。
23、函数
f(x)=x3+6x2+9x
，那么（ ）
（A）
x=−1
为
f(x)
的极大值点 （B）
x=−1
为
f(x)
的极小值点
（C）
x=0
为 的极大值点 （D）
x=0
为 的极小值点
【答案】B
【解析】从选项中可以看出，本题是要求函数的极值，因此我们对该函数进行求导，得到：
f'(x)=3x2+12 x+9=3(x+1)( x+3)
，
f' ' (x)=6x+12
。
由
f'(x)=0
得到两个驻点
x=−1
和
x=−3
。其中
f' ' (−1)=6>0
，
f' ' (−3)=−6<0
。
因此
x=−1
为极小值点，
x=−3
为极大值点。
24 、 设 函 数 在 开 区 间
(a , b )
内 有
f'(x)<0
， 且
f' ' (x)<0
， 则
y=f(x)
在
(a , b )
内 （
）
（A）单调增加，图像上凹 （B）单调增加，图像下凹
（C）单调减少，图像上凹 （D）单调减少，图像下凹
【答案】D
【解析】
根据函数增减性和一阶导数的关系，
f'(x)<0
，故函数在
(a,b)
内单调减少；
根据函数凹凸性和二阶导数的关系，
f''(x)<0
，故函数在
(a , b )
内为凸函数。因此选择 C。
25、设函数 在区间
[
0, a
]
上有连续导数，则定积分
∫0
ax f '(x)dx
在几何上表示（ ）
（A）曲边梯形的面积 （B）梯形的面积
（C）曲边三角形的面积 （D）三角形的面积
【答案】C
【解析】
由分部积分法可知：
∫0
ax f '(x)dx =∫0
axdf (x)=xf (x)|
0
a−∫0
af(x)dx =af (a)−∫0
af(x)dx
。
根据定积分的几何意义可以得到如下图形，阴影部分则是最后表示的部分。因此为曲边三
角形的面积。
)(xf )(xf
)(xf
)(xfy
))(,( afa
)(xfy
26、设
A
和
B
均为
n
阶矩阵（
n>1
），
m
是大于 1 的整数，则必有（ ）
（A）
(AB )T=ATBT
（B）
(AB )m=AmBm
（C）
|ABT|=|AT||BT|
（D）
|A+B|=|A|+|B|
【答案】C
【解析】
由矩阵乘法转置的运算法则可以知道：
(AB )T=BTAT
，而一般情况下，矩阵的交换律是
不成立的，即：
AB≠BA
。也就是说 A 项是错误的。
同样的道理，对于 B 项，
(AB )2=( AB )(AB )≠A2B2
，因此 B 项也是不成立的。
在行列式的运算中，
|A+B|=|A|+|B|
一般也不成立。
对于 C 项，根据行列式的运算法则有：
|ABT|=|A||BT|=|AT||BT|
，故选择 C。
27、设线性无关的向量组
Z1
，
Z2
，
Z3
，
Z4
可由向量组
β1
，
β2
，…，
βs
线性表示，则
必有（ ）
（A）
β1
，
β2
，…，
βs
线性相关 （B） ， ，…， 线性无关
（C）
s≥4
（D）
s<4
【答案】C
【解析】
根据定理可知，若向量组
α1, α2,⋯, α s
可以由向量组
β1, β2,⋯, βt
线性表示，且
α1, α2,⋯, α s
线性无关，则有：
s≤t
。故选择 C。
28、若线性方程组
{
x1−2x2+3x3=1¿¿¿¿
无解，则
k=
（ ）
1
β
2
βs
β
相关推荐
-
小升初名校奥数真题及答案VIP免费
2024-11-09 27 -
七年级下册地理第四章试卷及答案人教版VIP免费
2024-11-10 40 -
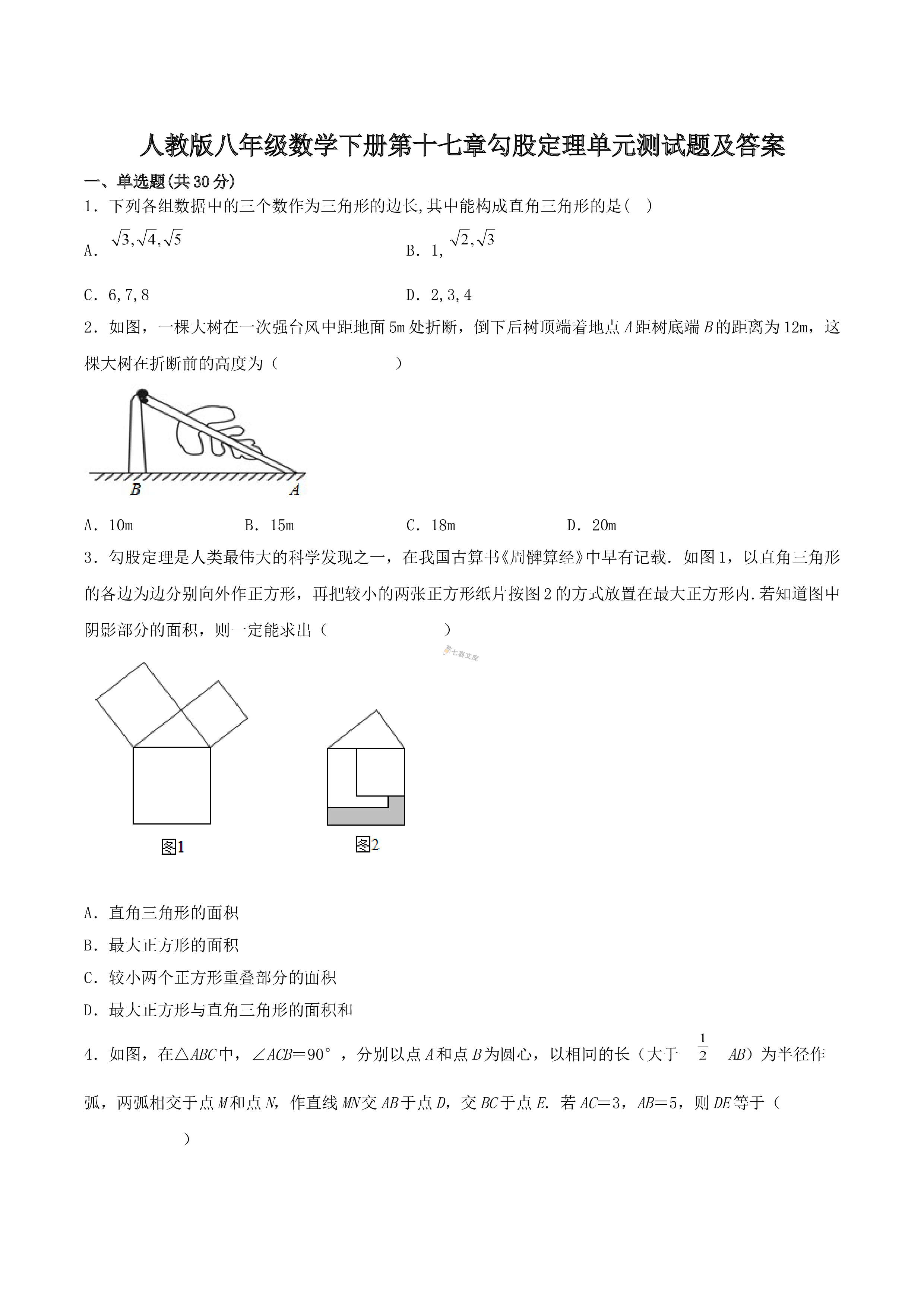
人教版八年级数学下册第十七章勾股定理单元测试题及答案VIP免费
2024-11-10 402 -
2011年成人高考专升本生态学基础考试真题及答案VIP免费
2024-11-12 31 -
2023年武汉工程大学教育管理学考研真题VIP免费
2024-11-14 9 -
2018年普通话考试真题VIP免费
2024-11-24 7 -
2017年普通话考试真题VIP免费
2024-11-24 4 -
2016年普通话考试真题VIP免费
2024-11-24 2 -
2014年普通话考试真题VIP免费
2024-11-24 5 -
2015年普通话考试真题VIP免费
2024-11-24 6
分类：行业题库
价格：3.3金币
属性：7 页
大小：257.05KB
格式：DOC
时间：2024-11-14
